uzasy1

Вспомним - с чего начинается объяснение магнетизма в школе- нам рисуется соленоид с изображением силовых линий "магнитного поля" (рис.1).

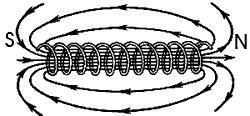
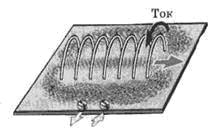
Рис.1. Изображение силовых линий соленоида и его иллюстрация с помощью железных опилок.

Вот первый шаг в сторону от науки: силовые линии магнитного поля не могут проходить по столь замысловатым кривым, - они проходят по линиям напряженности- то есть, -по окружностям вокруг проводников. А рисунок справа дает нам векторную сумму действующих силовых линий от всех проводников. В голове школьника уже утеряна информация о векторе напряженности, там остались опилки, расположенные "по силовым линиям".

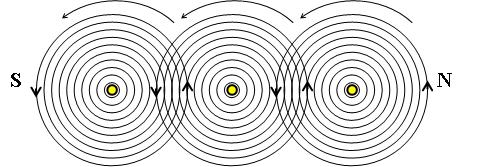
Рис.2. Реальное расположение силовых линий вокруг витков соленоида.

А вот так надо было преподносить (рис.2). Между витками соленоида напряженность равна нулю из-за противоположности векторов. На поверхности катушки эти векторы совпадают, образуя неправильные овалы. Если же вместо стрелок окрасить силовые линии по противоположным векторам, мы получим подобную картину и для соленоида (рис.3). Столь немудреным способом легко объяснить школьникам особенности соленоида, включая происхождение "краевых эффектов", без искажения смысла терминов.

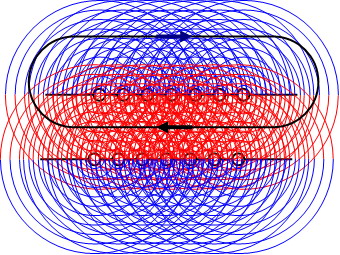
Рис.3. Иллюстрация векторного сложения магнитных сил соленоида.

Если внимательно рассмотреть эту картинку, обнаруживаем, что снаружи катушки поля разного знака, т.е. при малых размерах катушки вторичную (повышающую) обмотку трансформатора целесообразно размещать внутри первичной обмотки. А внутри соленоида нет напряженности противоположного знака. Это и есть реализация трансформатора Тесла, в котором выходное напряжение превышает расчетное на 60-70%.
На рис.4 приведены эпюры магнитной напряженности внутри соленоида.

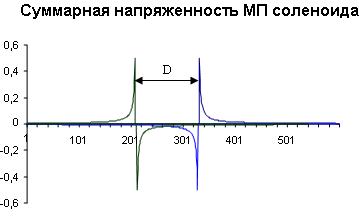
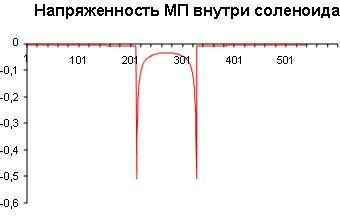
Рис.4. Диаграммы напряженности магнитного поля в соленоиде.

А правый рисунок показывает, что такая эффективность трансформатора Тесла сохраняется в тонком слое, прилегающем к виткам первичной обмотки. Следим за мыслью Николы Тесла: трансформатор должен быть бескаркасным -это раз. Намотать высоковольтную обмотку с большим числом витков можно лишь очень тонким проводом - это два, причем катушка должна быть вытянутой, чтобы разместить большое число витков в тонком слое -это три! Всё это и создает важнейшие признаки трансформатора Тесла.
Пока мы перечислили простые непонимания, а имеются ли радикальные заблуждения существующей физики в этом вопросе?
- Да, есть. Какая теория скажет вам, что выигрыш трансформатора Тесла напрямую связан с диаметром провода первичной обмотки? А ведь крутизна спада напряженности (соответственно - и толщина выигрышного слоя) определяется радиусом провода

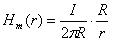^{( 1).}

Да, радиус провода математически сокращается, но это тот случай, когда математику надо поверять логикой [1] - выражение 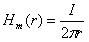( 2)

^{( 2).}

позволяет рассматривать невозможное сочетание , когда магнитное поле перемещается из воздушного пространства в металл. А при таком сочетании не только изменяется магнитная проницаемость среды, при этом меняется значение тока, определяемого потоком электронов в указанном радиусе сечения проводника. Значит, общепринятое уравнение (2) надо записывать иначе

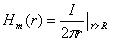^{( 3).}

А как вам нравится утверждение учебников, что внутри соленоида силовые магнитные линии имеют равномерную плотность? Оцените глубину этого заблуждения по правой диаграмме рисунка 4. Тесловский эффект лежит в чрезвычайно малом диапазоне расстояний. Да, с натяжкой можно говорить о квазипостоянстве магнитной напряженности, но каков по значимости эффект, не учитываемый наукой, но используемый Тесла? Допустимо ли так упрощать знания?
Еще глубже заблуждения современной физики в примерах с магнитопроводами. Но, чтобы перейти к этому разделу, необходимо рассказать сущность магнитных сил. Лучше это понять из анимационного сайта [2], где очень кстати и устройство электрона показано.

2. ИНДУКТИВНОСТЬ

Но прежде нам предстоит понять - что есть индуктивность. Как возникает ее свойство инерции для тока? Ведь, индуктивность и взаимоиндукция - это параметры формального описания процессов, не имеющие физической интерпретации. Достаточно сказать, что индуктивность катушки (рис.1) связана с ее конструктивными параметрами странной эмпирической формулой

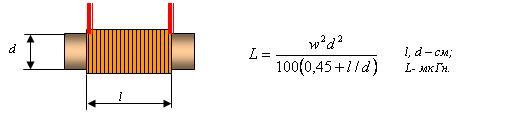
Рис.5. Однослойная катушка индуктивности.

Здесь W- число витков катушки, - явно доминантный параметр. Но отчего он во второй степени и как он определяет инерционность процессов. Инерция тел рождается при их движении в пространстве. Нужно быть полным слепцом, чтобы не замечать, что катушка индуктивности получает эти свойств во взаимодействии со свободными электронами пространства. Что кинетическая энергия летящего тела mv²/2, что энергия индуктивного накопителя Li²/2 - это половинки полной энергии (сравните с E=mc²).
Достаточно рассмотреть появление индуктивности при "плавном" изменении числа витков w от 0 до 1 (рис.6), чтобы несказанно удивиться невнимательности физиков.

Рис.6. Постепенное приобретение индуктивных свойств проводником.

    Ведь, придание формы витка влияет только на концентрацию силовых линий поля в пространстве внутри соленоида. Пространственные электроны могут поглотить энергию магнитного поля, лишь получая ускорение. Для этого на них должна действовать магнитная сила. Текущая скорость их движения пропорциональна магнитной напряженности, т.е. - току и числу витков. А квадрат числа витков получается за счет того, что соседние витки действуют на тот же объем пространства, т.е. при повышении плотности силовых линий.
    Мы также видим, что понятие "на тот же объем" условное. Витки чуточку смещают ареал действия магнитного поля. С учетом этого эффекта индуктивность оказывается функцией длины катушки. А дополнительная дробь в знаменателе отражает краевые эффекты, где суммируется действие не всех витков.
    Естественно, возникает вопрос: а что произойдет с индуктивностью, когда свободные электроны приобретут большое ускорение?
    - Сопротивление среды упадет и она не сможет отбирать половину энергии поля.
    -Значит, индуктивность исчезает во времени?
    -Можно и так сказать, просто надо сменить направление тока. Вот поэтому мы и получаем индуктивное сопротивление катушки 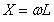, которое зависит от частоты изменения тока.