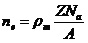
where
- volume density of metal (kg/m3),
Z - valence of a chemical element,
Na - the Avogadro constant,
À - relative atomic mass of element.
According to our research, the volume concentration of electrons in solids, in fact, proportional to the volume density of materials and mediums. Research carried out for air, allowed us to calculate the distance between the free electrons
m. or
the
volume density of charges
.
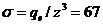
Accordingly,
for an
arbitrary environment
this value
should be
multiplied by the ratio of densities
.
But more often the other way is more convenient
, leading to the atomic
structure of the material. So, if the period of the atomic grid b is
known, we immediately sort out - how many cells of the grid lie between
the free electrons. For example, in the copper atom
m, and 
m. So, n=19,4.Lets take simulated copper conductor with cross-section z ^ 2 and 1 m long. In this section will be n ^ 2 = 376 atoms. This is a very "handy" conductor because te current in it creates a single electron in the section.
Lets find the resistance of the conductor
Ohm.Define the density of current
and find the current
Determine the required voltage U=IR=0,01756 Â,
as well as power in the circuit N=UI=8,6229E-13 Wt.
The electric field at such length is numerically equal to the voltage
H=0,01756 (Â/ì).
This tension creates a Newtonian force acting on the electron
Since this is a
movement
of a single electron,
we can find the
time of
passing the electron-electron
distance z
and
find out the velocity of electrons
-Here's the real velocity of the electrons in copper. The first problem is solved and with the substitutions we get a nice formula for the mean velocity of electrons
There is a second problem. It is due to the fact that current is proportional to the voltage, and speed. But tension creates Newtonian force, and it creates acceleration
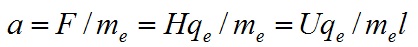
Consequently, the current may be proportional to the velocity of the electrons only under one condition, that their velocity periodically resets to zero
(Fig.2
of part 2 ). In this
case, the
current is characterized by
a length
L of the free path
of
electrons and can be
found
from the
condition
or
The current in the metal may be proportional to the tension only along the periodic discharge of kinetic energy. Frequency of discharges associated with the grid structure and packing density of atoms. Characteristic of frequency - electron free path length L
Thus, for copper the length of free path was found to be
. It is interesting
to note
that it
is
L / b =
8,26 periods of
atomic
structure. Finally, consider the
fundamental
aspects of
energy.
First,
we
calculate the kinetic energy
of one
electron
If we consider all the electrons in the 1 m length of conductor 1 / L, then
This energy is exactly equal to the work of force F on the length of the conductor. Time for us to remember that originally the entire conductor had the same potential. Therefore, there couldn't be potential distribution along the length of the conductor. Initially, a standard distribution of the field potential from the electrode of source of tension, affects only the nearest atoms of conductor end. Change of the atoms potential dU changes their energy to dE = q dU. Because each metal atom has a certain volume, we can talk about increasing the energy density from one end of the conductor. This pressure is determined by the magnetic forces of the field of atomic energy. Only now becoming possible movement of free electrons. This movement transmits energy through transmitting the energy to remote atoms. For some time the pressure wave creates a uniform potential gradient. Only after this conductor starts conduction. That's the source for inductive properties of the linear conductor!
Finally, we can find a functionality for the resistivity
It is noteworthy that the resistivity is proportional to the square of the bulk metal density and inversely proportional to the length of free path.
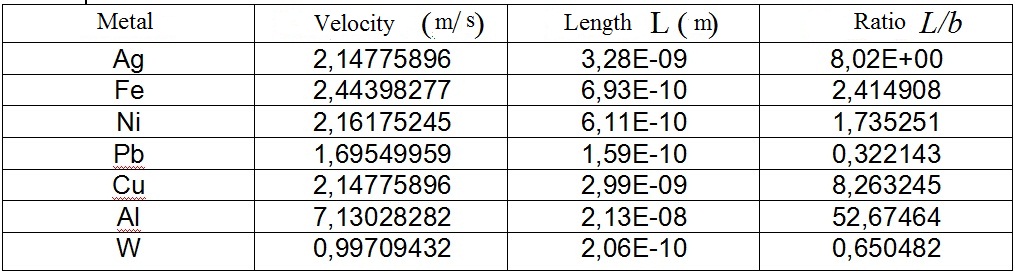
As an illustration of these results, we present the calculated values of electron velocities for some metals, as well as the length L of the free path and the ratios L / b.
References:
1. Drude P., Zur Elektronentheorie der Metalle. - Ann. Phys., 1900, Bd. 1, S. 566;
Back
