It turns ungracefully: a man uses electric current a third century, thousands of books written about it, and in 2009 we have to forget everything and start over. The concept of "current" man formulated by studyingelectricity in conductors. And now we're trying to "unbind" this concept from conductors and, of course, come to a deadlocks.
In the first part, we found an important thing: the vortex magnetic field around the conductor is determined by the degree of orientation of the electron velocity vector. A degree of orientation depends on the ACCELERATION of electrons. But the paradox isthat the current
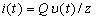is
proportional
to the velocity.
How can
this be connected?
The logic
is
inexorable: it is possible
in a
single case, where the
uniformly
accelerated motion of
electrons is preserved
only
over
short distances
of b
path.
Then
the
average speed will be
proportional
to the
acceleration. Figure 2
shows a
graph of the
velocity of this motion.
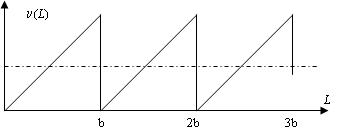
Fig.2. Characteristic of electrons velocity changing in conductors.
In order to leave the current proportional to the velocity, it is necessary that the segments b would be small and uniform. The slightest irregularity of segments leads to the nonlinearity of given energy mv ^ 2 / 2. Then the potentials in the conductor would be uneven, which would inevitably lead to local overheating of the conductor. So we get another condition to define a medium as an electrical conductor - the uniformity of the distribution of potentials. In metals, this condition is satisfied automatically due to the strict periodicity of the crystal grid. And in dielectrics?
Yes, condenser paper can not be considered uniform in structure. But the synthetic films and oxides are uniform, at least at the macro level. Consequently, the uniformity condition is not enough. There is another factor, that sorts more reliably the materials conductivity. Let's look at a picture of lightning.
Fig.3. Stochastic way of lightning strike.
Sounds familiar? Loss of primary direction and search for the best branch of conductivity. - Here is an example of the uneven distribution of potentials. And it's additional sign-energy of the particles field on the way of electrons. It is the field of the particles energy (including atoms and molecules) that determines the resulting potential of the field
.
Then, for
the atomic
lines
of
conduction in the metal
the
pattern of energy fields will be
the same
as shown in Figure 4.
Fig.4. Energy fields of atoms in metals.
If summarize the effect of the fields, the nature of the resultant field will remain, but the lower limit will be higher. Lets denote this minimum (threshold) through E (Fig. 5).
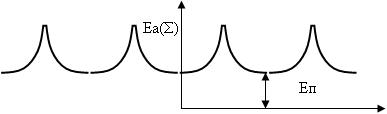
Fig
5.5. The
total interatomic energy field in metals.
That is what electrons must overcome. Here is one subtlety: the energy expended in overcoming the barrier, then returns to the electron, but to overcome the first obstacle electrons must obtain energy from the outside (Fig. 6).
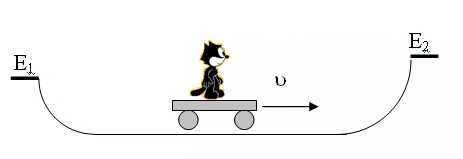
Fig.6. The image of a skateboard in overcoming the energy barrier.
Then the returned energy will be spent on the next rise, and so on, increasing the energy strictly by EQUAL increments dE. And so the potential of the conductor varies in strict proportion to its length. That is not achievable in dielectrics.
You may ask "why?" - In fact, modern physics gives us a rule for finding the strength in dielectrics as the ratio of the applied tension to the thickness of the dielectric
.
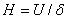But
this is one of the biggest misconceptions, as in
the absence of current, potential of the atom remains
unchanged (on the left in Figure 4). And
the intensity of falling energy field is equal to several million volts
/ meter. Increasing
the applied voltage can overcome this barrier, but then
returned huge energy would accelerate electron so
that there would come a 100% probability of collision with atoms and
molecules. Tremendous
released
energy
locally burns fragment of environment. This
is the electrical breakdown of the dielectric, when the avalanche
increase in current leads to the burning of small parts of the path. You
can easily verify that the sample with a lightning is appropriate and
the nature of dodging of breakdown currents, and the final effect are
the same.Thus, dielectrics - a class of materials characterized by large interatomic distances and strong atomic (molecular) fields. Atomic field in metals by 2 orders of magnitude lower due to the strong interatomic bonds. For example, the energy of the free iron atom is of the order E-17 J, and of bound atoms ~ E-19 J. The difference between these values is spent on the mutual attraction of the atoms.
